Almost everyone knows the rules to the popular children's card game Go Fish. However, far fewer individuals know the rules to the Quantum version of Go Fish, which is not a children's game at all. In Quantum Go Fish players use principles from Quantum physics to determine the makeup of the hands. Thus, this game can be not only a fun and challenging logic type game, it can also be used to help illustrate some of the basic concepts of Quantum Physics.
Although unknown where this game first originated, it has experienced recent times of popularity at the University of Berkeley and, as such, probably was developed by some of the resident geniuses attending or instructing at the University. The game can be played by almost any number of players, but is usually best with 3 to 5 (with fewer than 3 it can be a very simple game and with greater than 6 participants, it can often get very confusing remembering the status of everyone's hand).
The basic concept of the game is that each player starts with a hand of four unknown cards and through the course of the game, in asking questions and responding to questions from other players, they reduce the uncertainty of the identify of each hand. Because no one ever actually sees his or her cards, no cards are actually needed to play, with most games requiring each player to mentally recall and calculate not only his own hand, but that of the players, entirely in his or her own head. To simplify this calculation and recollection some players include the use of various methods or objects to assist in that capacity (see below). There is no actual dealer, and thus any method can be used to determine the player to have the first turn, and the turns then continue in a clockwise direction around the table from player to player.
The game does have some similarities to the normal game Go Fish, which gives rise to this game's name. (For the instructions to the classic children's game of Go Fish, click this link.) As mentioned, however, no actual cards are needed, and some play that each player uses four fingers to represent the number of cards in each player's hand. To begin, it is assumed that each player has a hand of four unknown cards. The hypothetical deck from which these cards have been dealt is considered to have exactly the same number of sets of four cards as participants in the game. Thus, if the game is played by three players, there are considered three such sets of four exact matching cards (these sets are usually called suits).
On his turn a player simply asks any other player in the game for a specific suit of card. As mentioned previously, a suit represents a type or rank of card of which there are exactly four distributed amongst the player's hands. These can be represented by anything, and the first player to ask for a particular suit can make up any name for that suit (such as platypuses or cranberries), after which time that suit will be called by that name for the remainder of the hand. A player may never ask for a card of a suit for which he has no such cards, and thus, by asking for such a card he has immediately "determined" that he himself also has at least one such card in his own, unexposed hand. Thus, from that moment, his hand will be considered to have at least one card of the requested suit.
Meanwhile, the player who is asked for such a card then determines if he has such a card. If that player has already been determined (from previous plays) to have one or more cards of that suit, he must give one such card to that player. If he still has cards that have the possibility of being that suit, but have yet been determined to be of that suit, he may elect, at his option to state that he does or does not have cards of that suit. If he indicates he does have cards of that suit, he does not state how many he has but must give exactly one card (considered of that suit) to the asking player. This then, of course, determines that this card "passed", is of the suit requested. If the player states that he has no such cards, this also determines that his hand then consists of no cards of the requested suit (which also stipulates that this player may never ask for such cards of that suit for the remainder of this hand). In the normal game in which players keep track of all the hands mentally, no actual cards are used or passed to other players.
The game continues in this way until one of several possible outcomes are realized through play of the hand:
- If, by logic, one player is discovered to have all four cards of one suit, the hand ends with that player immediately declared the winner.
- If, at the end of any player's hand, the identity of every card in the game has been determined, that last player is declared the winner (that player is said to have collapsed the waveform and thus removed all uncertainty).
- If a player creates a paradox, the game immediately ends and ALL players are considered to have lost the game, with no winner in that hand. A paradox is the case in which a player, either in asking a question or responding to a question creates an impossible arrangement of the cards (such as forcing a configuration in which there are too many suits, or there are more than four cards of the same suit).
One method that can assist in this way is the use of actual cards. Using this method, one set of four equally ranked cards should be set aside, which will represent cards as known. In addition, each player is dealt four other random cards from the deck, which are simply placeholders to represent a card that player holds. As players are "discovered" to have a specific card, one of the face down cards should be replaced by one of the actual cards representing that rank of card. The player who was asked for the card, would then pass this face-up card to the asking player. Thus, as the identity of certain cards are discovered, they would be replaced with the actual card rank represented.
As this game can seem confusing at first for new players, a detailed description of an example game should greatly assist those new to this game and it's concepts.
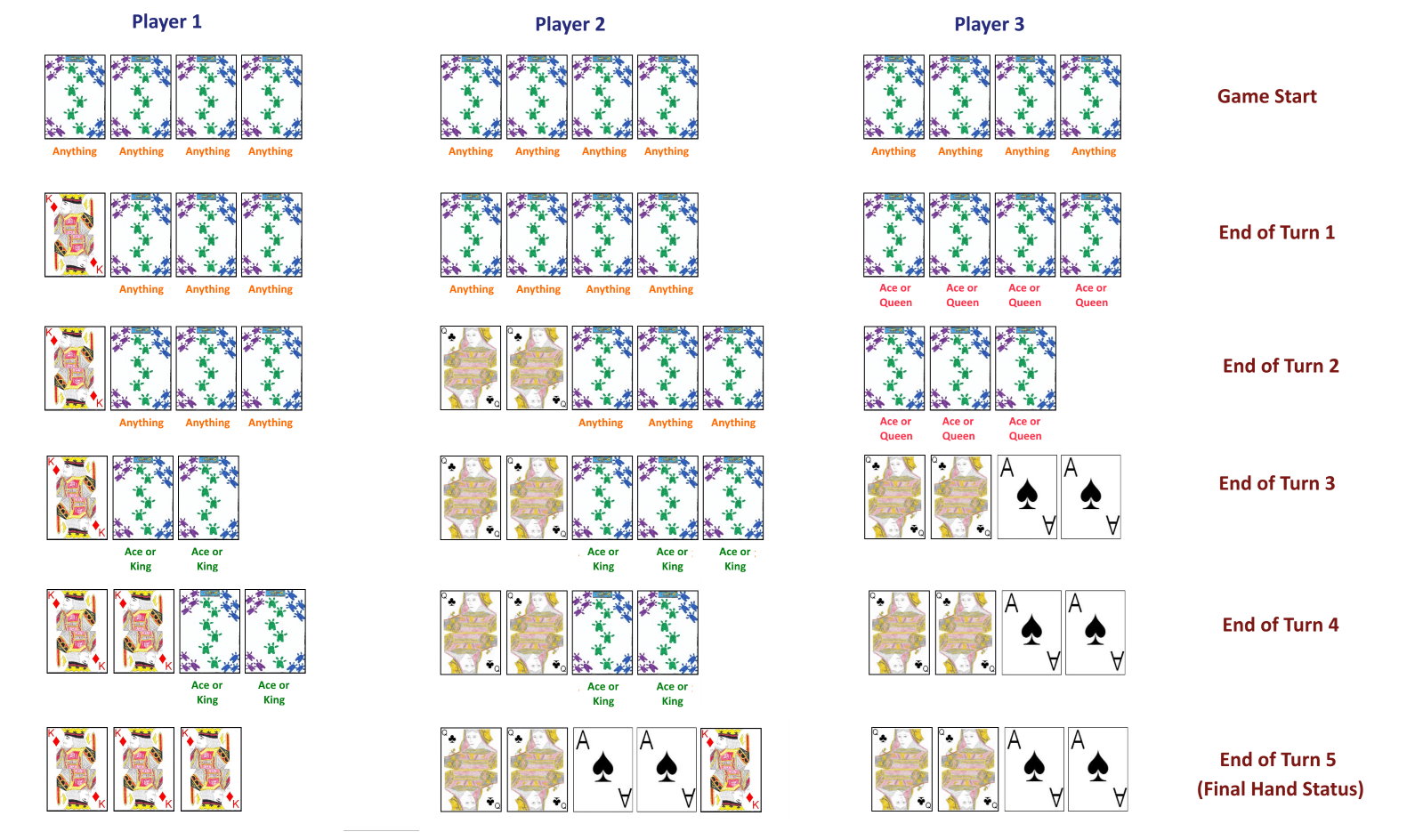We will suppose, for this example that there are three players in the
game. The "suits" to be used in this example, for each of illustration
will be a rank of card from a standard card deck. Thus, the deck from
which the hands will be dealt consists of exactly four Kings, four Queens and four Aces.
Thus at the start of the game, each player has four cards, in which no cards held by any players are yet determined.
Player 1 begins the game, with the first turn. On his turn he asks player 3, "Do you have any Kings?" In asking this question, Player 1 has asserted that he does have at least one such King. Player 3 then decides if he does or does not have any Kings. For this example, we suppose he says he does not have any Kings. Thus, we have the configuration as shown (Player 1 definitely has at least one King, with his other three cards being anything. Player 3 has four cards which can be anything except Kings).
Next, Player 2 has his turn (second turn in the game). He asks Player 3, "Do you have any Queens?" Player 3 indicates that he does, in fact, have at least one Queen, and thus one Queen is "passed" to Player 2. The layout of the hands is then as shown. Player 1 definitely has 1 King, and his other three cards can be anything. Player 2 has at least two Queens (at least one to allow him to ask for a Queen, and another passed to him from Player 3). Player 2's other three cards can be anything. Player 3 has three cards which can be anything except Kings.
Player 3 then has his turn. He asks Player 1, "Do you have any Queens?" (which indicates that Player 3 has at least one Queen remaining in his hand). Player 1 says that he does have a Queen and "passes" it to player 3. The state of the hands, at the end of this turn is thus: Player 1 has one King. His two remaining cards are either Aces or Kings, since all four Queens have now been accounted for. Player 2 has two Queens, his remaining three cards can be anything except Queens. Player 3 has two Queens, his remaining two cards must be Aces (since he previously stated he did not have any Kings and player 2 has the remaining two Queens).
Player 1 then has his second turn. Player 1 asks Player 2 "Do you have any Kings?" Player 2 states he does have such a card, passing it to player 1. The configuration of the cards is as follows: Player 1 has two Kings, his two remaining cards can be a combination of Kings and Aces. Player 2 has two Queens as previously determined, and two other cards which cannot be Queens (as Player 3 has the remaining two Queens). Player 3's hand has been previously determined to be two Queens and two Aces.
Player 2 has his second turn. On his turn he asks Player 1 "Do you have any Aces?" Player 1 indicates he does have one Ace and passes it to player 2. The final configuration of hands for each player would thus be as follows. Player 1 has three Kings (Two determined during previous plays and one by process of elimination since all other cards have been specifically determined). Player 2 has two Queens, two Aces and one King (two Queens determined from previous plays and two Aces determined from his request and card received. His last King by process of elimination since all other cards have been previously determined). Player three has two Queens and two Aces, determined from previous plays during the hand. After this play, the identities of every card has thus been determined, with player 2 winning the game as the player who was able to remove all uncertainty, determining the exact composition of each card in every hand